задача об оптимальном соединении и разветвленные геодезические

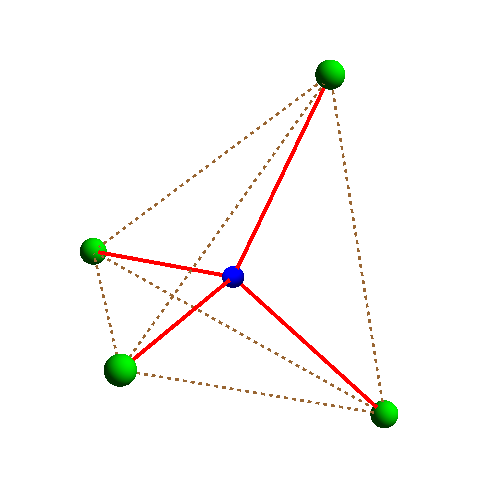
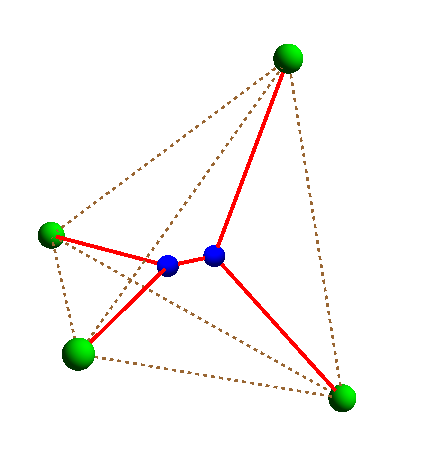
Четыре большие зеленые точки на рисунке — вершины правильного тетраэдра. Четыре отрезка соединяют их с маленькой синей точкой в центре тетраэдра, образуя сеть с одной дополнительной вершиной. Вопрос: можно ли соединить вершины тетраэдра более короткой сетью? Ответ: сеть можно укоротить, расщепив дополнительную вершину степени 4 на две степени 3 (на рисунке маленькие синие точки). Возможность такого расщепления вытекает из общей теоремы о локальной структуре кратчайшей сети, согласно которой угол между смежными ребрами кратчайшей сети в Rⁿ (на самом деле, даже на римановом многообразии) не может быть меньше 120°. Поэтому степень любой вершины не превосходит трех. Это простой пример из теории минимальных сетей на поверхностях, имеющей обширные приложения, см. монографию А.О.Иванова и А.А.Тужилина «Теория экстремальных сетей» (Москва-Ижевск: Институт компьютерных исследований, 2003). См. также задачи на сайте кафедры.