взаимные превращения фигур и криволинейные координаты

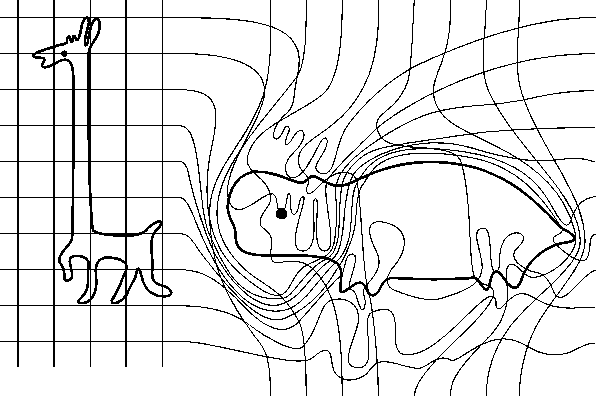
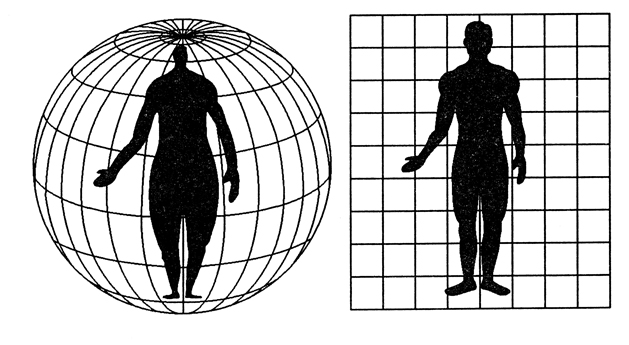
В физике и математике огромную роль играют регулярные криволинейные координаты (диффеоморфизмы). Такие координаты определяют семейства координатных линий. Если координаты декартовы, то координатные линии — прямые, параллельные координатным осям в евклидовом пространстве; они образуют ортогональную сетку. Изображение координатных линий позволяет наглядно представить соответствующий диффеоморфизм. Например, при диффеоморфизме жираф может «превратиться» в бегемота, см. рисунок. Еще один пример. При проекции Меркатора локсодромы, т.е. линии, пересекающие меридианы под постоянным углом, переходят в прямые линии на плоскости. При такой криволинейной замене координат геометрические фигуры заметно меняются, см. рисунок.