переворачивание подбрасываемой книги и гамильтоновы интегрируемые системы

Подбросим книгу вверх, как показано на рис. (а), закрутив ее вокруг горизонтальной оси. Поймаем ее и посмотрим, в каком положении она оказалась. Оказывается, результат зависит от того, как мы ориентировали книгу вначале. У нее есть три оси симметрии. Если закрутить ее вокруг оси, отвечающей наименьшему или наибольшему моменту инерции, то книга вернется назад в том же положении, какое занимала до броска. Но если мы закрутим книгу вокруг оси, отвечающей среднему моменту инерции, то книга перевернется: если сначала корешок книги был в левой руке, то поймав книгу, вы обнаружите, что корешок оказался в правой руке (рис. (b)). Этот красивый эффект, оказывается, является следствием скрытых симметрий в интегрируемой гамильтоновой системе, известной как случай Эйлера в динамике тяжелого твердого тела. Интересно, что 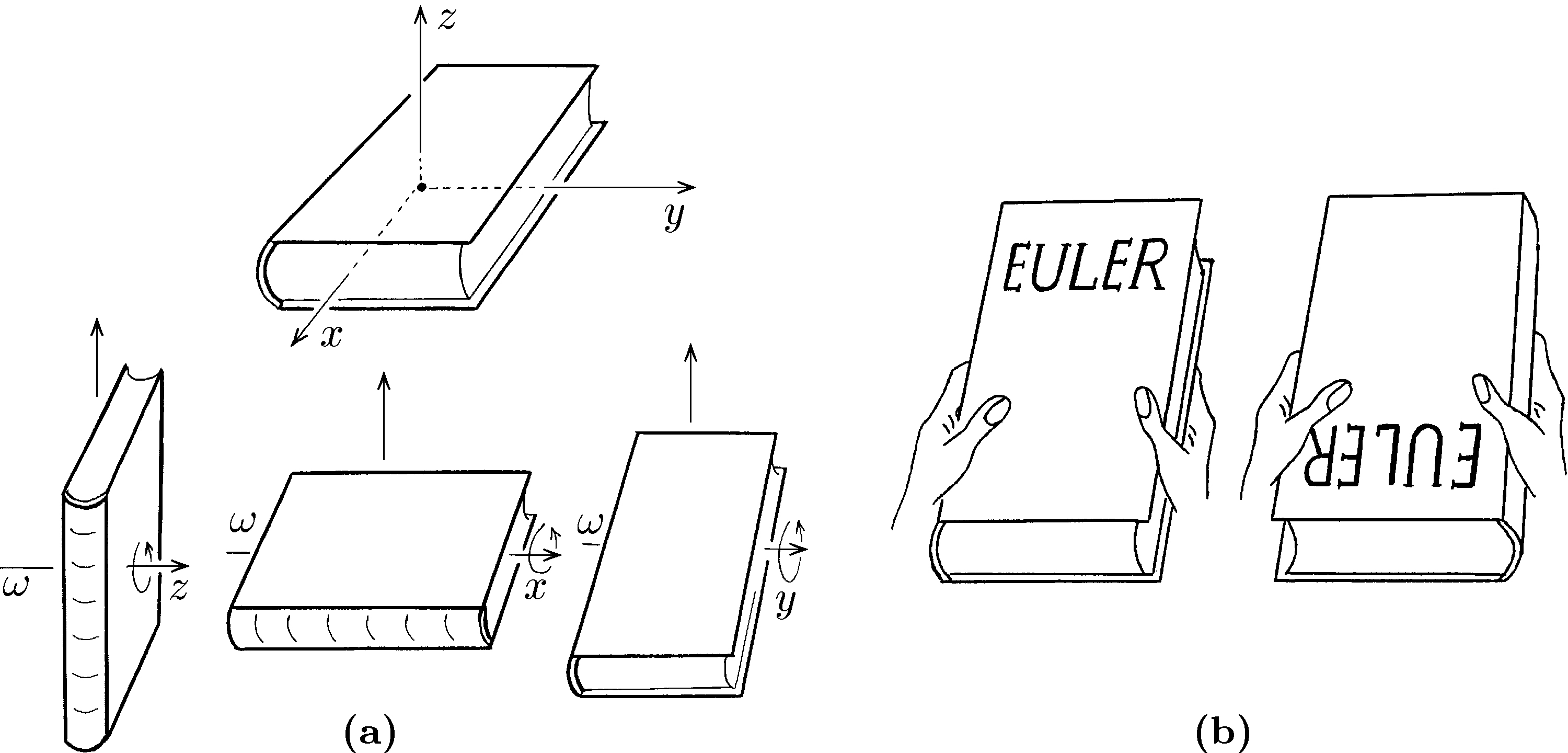то же объяснение лежит в основе причудливого движения «гайки Джанибекова» в невесомости. Ясно видна очень быстрая, почти скачком, смена ориентации гайки. Этот эффект связан с устойчивостью и неустойчивостью траекторий нашей динамической системы. Современная теория классификации гамильтоновых уравнений объясняет поведение многих других реальных физических и механических систем. См. книгу А.В.Болсинова и А.Т.Фоменко, «Интегрируемые гамильтоновы системы», т.2, гл.5:3.